|
|
|
Ces
deux programmes ne fonctionnent qu'avec Internet explorer 5.0 au
minimum. Si vous avez Nescape envoyez un message pour recevoir la version excel
Exercice N°1 : Faites les exercices que vous voulez. Complétez les cases bleues. Niveau collège
Exercice N°2 : Faites les exercices que vous voulez. Complétez les cases bleues et vertes. Niveau lycée.
Les solutions sont calculées à 0,1 près.
 |
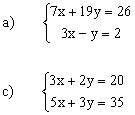a) S = { (1 ;1) }
c) S = { (10 ;-5) } |
 |
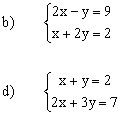b) S = { (4 ;-1) }
d) S = { (-1 ;3) } |
 |
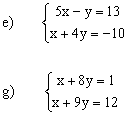e) S = { (2 ;-3) }
g) S = { (-87 ;11) } |
 |
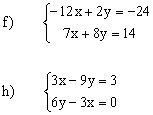f) S = { (2 ;0) }
h) S = { (-2 ;-1) } |
: Attention pour l'exemple h) , pour
la deuxième équation les variables ont été permutées.
: Attention définir x et y .
Soit x le nombre de billets de 50€ et y le nombre de billets de 100€.
On sait qu'il y a 12 billets au total de 50 et 100€ : donc x + y = 12
Dans le problème on parle par la suite de la valeur en € des billets qui s'élève à 1000€.
Si 1 billet de 50€ vaut 50€ alors x billets de 50€ valent 50x €.
De même pour les billets de 100€, comme il y en a y donc la valeur est 100y €. Soit au total tous les billets additionnés ont pour valeur 50x + 100y et on doit avoir 1000€ d'où 50x + 100y = 1000.
Donc on présente le système suivant :
Après calcul x = 4 et y = 8. D'où dans la caisse il y a 4 billets de 50€ et 8 billets de 100€.
Notons par exemple x le prix d'un orangina et y le prix d'un coca en €. Le prix payé à la première table est :
3x + 2y = 5,5
Pour la deuxième table, le prix payé est de x + 3y = 4 .
Donc
le système est le suivant :
.
le couple ( 1,5 ; 1 ) est solution : x = 1,5 € et y = 1 €.
a)
Soit a le nombre de billes d'Antoine et t le nombre de billes de Thomas
Antoine dit à Thomas : " Si tu me donnes 6 billes, j'en aurai autant que toi ". Car Thomas donne 6 billes donc il a t-6 billes et en conséquence Antoine en a 6 de plus donc a+6 billes
Thomas réplique : " Si je t'en donne 10 , tu en auras 2 fois plus que moi ".Car Thomas donne 10 billes donc il a t-10 billes et en conséquence Antoine en a 10 de plus donc a+10 billes. De plus Thomas en aura deux fois plus qu'Antoine donc a+10 = 2(t-10).
b) le système
est donc équivalent à
.
Car il faut développer, mettre les variables du même côté et les nombres
dans le membre de droite. Ceci étant dit on aurait plus utiliser la méthode
par substitution.
La solution est donc Thomas a 18 billes et Antoine en 6 de billes.
a) Après résolution x vaut 2 et y vaut 3,5.
b) Dans un premier temps définissons x et y :
Pour le badge N°1, il y a 5 triangles bleus et 3 triangles jaunes; comme la 1ère équation est 5x+3y=20, on est tenté de supposer que x est le nombre de triangles bleus et y est le nombre de triangles jaunes.
Pour le badge N°2, on 4 bleus et 4 jaunes. Donc on valide bien la supposition précédente.
On peut donc conclure qu'un triangle bleu vaut 2€ et un jaune vaut 3,5€.
Dans le badge N°3, il y a 3 triangles bleus et 5 jaunes ( Attention le carré jaune = 2 triangles jaunes). Donc le prix du badge N°3 est prix = 3*2+5*3,5=6+17,5=23,5€