Systèmes de deux équations à deux inconnues du 2ème degré
Définition :
On a toujours deux équations avec deux inconnues comme x et y., sauf que dans l'une des deux équations au lieu de présenter soit une addition ou une soustraction de termes on a une multiplication.
Méthode :
| La résolution fait appel à la méthode par substitution, c'est à dire on exprime l'une des deux variables en fonction de l'autre, puis on remplace cette équation dans la seconde. | |
| Lorsque l'on a remplacé une des deux équations, en développant on obtient une équation du second degré soit en x soit en y. | |
| Il ne reste plus qu'à la résoudre pour trouver soit aucune , une ou deux valeurs. ( Voir cours ) | |
| On utilise l'équation de départ pour trouver la seconde variable : Il se peut que l'on ait plusieurs couples de solutions. |
Exemple :
| Étapes | Calculs | Commentaires |
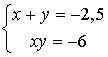 |
2 équations à 2 inconnues : une addition dans la première, une multiplication dans la seconde. | |
| Expression de x en fonction de y |
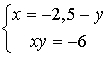
|
On a choisit x on aurait pu le faire avec y. Le principal est d'exprimer x en fonction de y ou y en fonction de x |
| Substitution dans la seconde équation |
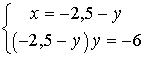
|
On remplace dans la seconde équation x par son expression trouvée dans la première équation |
| Développement |
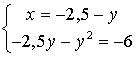
|
|
| Obtention de l'équation du second degré |
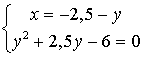
|
Toujours écrire l'équation du second degré sous la forme f(y)=0 |
| Résolution de l'équation du second degré à part |

|
Pour la résolution se reporter au chapitre des polynômes du second degré |
| Écriture des systèmes |

|
Il est important de revenir à une écriture de système. |
| Calcul de l'autre variable |
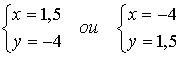
|
|
| Solutions |
|
Deux couples de valeurs sont solutions. |