Résolution algébrique d'un polynôme du second degré
| Résolution algébrique | |
| Exercices d'application. |
On partira obligatoirement avec
l'expression du polynôme du second degré ![]() .
.
Pour résoudre algébriquement ce polynôme on suit le diagramme suivant :
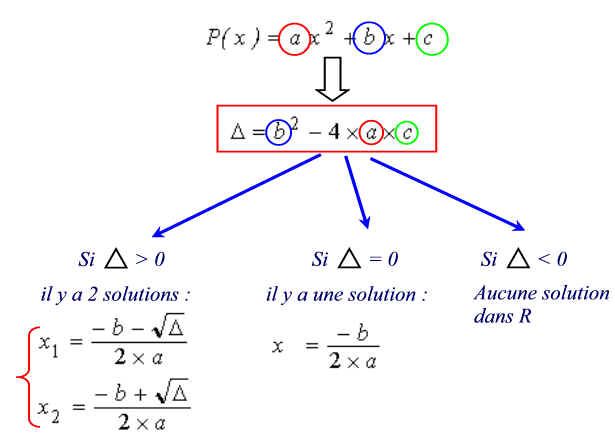
| Dans un premier temps on identifie bien les trois valeurs a, b et c. | |
| Ensuite on calcule le discriminant
| |
| Selon la valeur de ce dernier on a soit deux solutions dites simples, soit une solution double ou aucune solution ( notre étude étant dans R, il en sera tout autre sur l'ensemble des complexes ) |
Résoudre dans R les polynômes du 2nd degré suivant.
| Cas | P(x) | a | b | c | D |
|
Solutions |
| 1 |
|
- 0,5 | - 1 | 1,5 | 4 | 2 | x1 = -3 ou x2 = 1 |
| 2 | - 0,5 | - 1 | - 0,5 | 0 | 0 | x1 = - 0,5 | |
| 3 | - 0,5 | - 1 | - 1 | - 1 | // | aucune solution | |
| 4 |
|
1 | 0 | - 9 | 36 | 6 | x1 = -3 ou x2 = 3 |
| 5 |
|
1 | 4 | 4 | 0 | 0 | x1 = 2 |
| 6 |
|
1 | 1 | 1 | - 3 | // | aucune solution |