|
|
 |
 | Illustration de  |
| Exercices |
On définit par changement de variable le fait de transformer une équation fonction d'une variable en fonction d'une autre variable ( ATTENTION, x et X sont deux variables différentes ).
Les changements de variables ne sont pas uniques.
Exemple 1 : Soit f(x) la fonction
définie pour x > 1, par
.
On remarque que l'on peut faire le changement suivant X = x-1. Pour le dénominateur aucun problème on aura X, par contre pour le numérateur, il est nécessaire de faire quelques petits calculs.
| Comme X = x-1 |
| On a x = X+1 |
| Du
coup
 |
| Finalement
, nous n'écrirons plus f(x) mais f(X) :
 |
Exemple 2 : Soit la fonction k(x) définie sur 
,
par 
.
Faire le changement de variable suivant : X = x-4
| x = X+4 |
| k(x) devient
K(X) par
|
Définition :
| Soit f une fonction définie sur un intervalle I. |
| Soit J l'intervalle image de I par la fonction f. f ( I ) = J |
| Soit g une fonction définie sur J. |
| Soit K l'intervalle image de J par la fonction g. g ( J ) = K |
| La fonction définie sur I et qui, à tout nombre réel x de I,
associe
 est
appelée fonction composée de f par g
et notée
: |
ATTENTION
:
Voir exercice suivant
Exercice
Soit la fonction f définie sur
par
et g définie sur
par
Calculer
.
Calculer
.
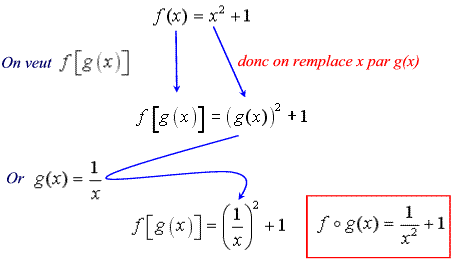
Dans
le 1er cas, on demande de calculer
.
On sait que ,
or on veut ,
ce qui revient à remplacer dans f la variable x par la
fonction g(x). Donc
Dans
le 2ème cas, on demande de calculer .
On sait que ,
on applique le même raisonnement que précédemment.
Comme
on le voit bien dans cet exemple
